What is the Treynor Ratio?

The Treynor Ratio measures the excess strategy return per unit of systematic risk. The Treynor ratio is one of many performance metrics that illustrates how much excess return was achieved for each unit of risk taken. While the numerator is the same as the numerator used for the Sharpe ratio, the denominator, which is how we adjust for risk, is different. The Sharpe Ratio adjusts for risk using standard deviation, which represents total risk, while the Treynor Ratio uses beta, which represents systematic or market risk. For more information on the Sharpe Ratio, please check out What is the Sharpe Ratio?

Treynor Ratio Formula

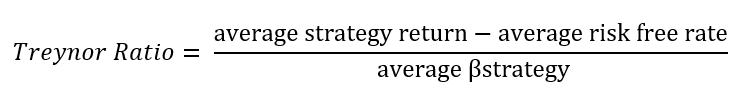
Annualized Treynor Ratio

When calculating this ratio using monthly data, the Treynor Ratio is annualized by multiplying the entire result by the square root of 12.

What is a Good Treynor Ratio?

The Treynor Ratio is a ranking device so a portfolio’s Treynor Ratio should be compared to the Treynor Ratio of other portfolios rather than evaluated independently.

Since the Treynor Ratio measures excess return per unit of risk, investors prefer a higher Treynor Ratio when comparing similarly managed portfolios.

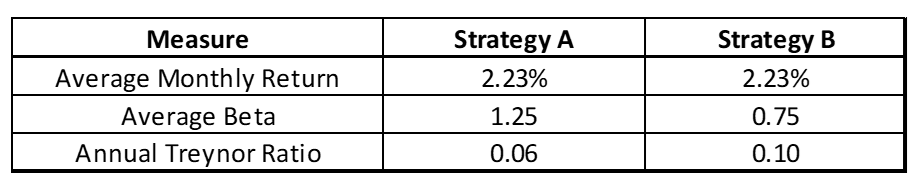
Example Treynor Ratio Calculation

Suppose two similar strategies, Strategy A and Strategy B, had the following characteristics over one year. For this period, the average monthly risk-free rate is 0.10%.

Please note that the Treynor Ratio calculated in this example is based on monthly data and, therefore, needs to be annualized to get the result. The full calculation is completed as follows:

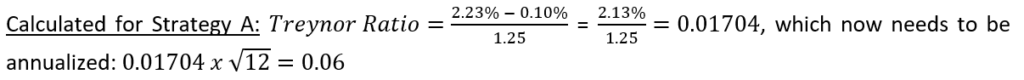
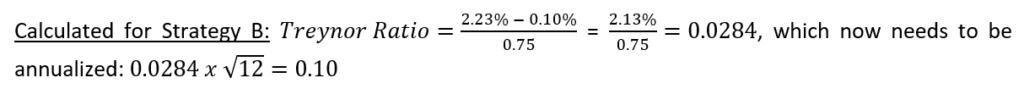
Although the strategies have the same average monthly return over the one-year period, the Treynor Ratios differ due to their differences in systematic risk (i.e., beta). That is, Strategy B is less sensitive to market movements, while Strategy A is more sensitive to market movements, indicating that Strategy A took on more systematic risk than Strategy B. Despite the additional systematic risk taken by Strategy A, the average monthly return achieved was the same between the two strategies. Therefore, Strategy B has a higher Treynor Ratio because it achieved a greater return per unit of systematic risk. Because Strategy B has a higher Treynor Ratio, it would be preferred over Strategy A for an investor deciding between the two.

How to Interpret Treynor Ratio

As mentioned, a higher Treynor Ratio is preferred. However, when comparing similar investments, a higher Treynor Ratio simply means it’s better. Holding everything else equal, there’s no way to interpret how much better. In other words, a Treynor Ratio of 0.50 is not necessarily twice as good as one that’s 0.25.

A key component to ensuring the Treynor Ratio is meaningful for the portfolio is to verify that the benchmark being used to measure beta is appropriate for the given strategy. In addition, the Treynor Ratio is difficult to interpret when it is negative (this can happen if there is a negative return or negative beta). Thus, the inputs must be positive to provide a meaningful result.

Why is Treynor Ratio Important?

The Treynor Ratio is important when assessing portfolio performance because it adjusts for risk. Comparing returns without accounting for risk does not provide a complete picture of the strategy.

The Treynor Ratio is widely used for strategies that will be added to a broadly diversified portfolio. When part of a broadly diversified portfolio, it is assumed that any unsystematic risk in the strategy will be diversified away, making it appropriate to focus only on systematic risk rather than total risk when “risk-adjusting” the returns.

Treynor Ratio Calculation: Using Arithmetic Mean or Geometric Mean

Because the Treynor Ratio compares return to risk (through Beta), Arithmetic Mean should be used to calculate the strategy return and risk-free rate’s average values. Geometric Mean penalizes the return stream for taking on more risk. However, since the Treynor Ratio already accounts for risk in the denominator, using Geometric Mean in the numerator would account for risk twice. For more information on the use of arithmetic vs. geometric mean when calculating performance appraisal measures, please check out Arithmetic vs Geometric Mean: Which to use in Performance Appraisal.